By Eli Shlizerman
Dynamical Systems theory is a powerful mathematical area which has been the bread-and-butter to many in the Applied Mathematics community. At UW AMATH, multiple courses, with dynamical systems as core methodology, are being taught from undergraduate to advanced graduate curriculum, and a variety of research directions both in foundations and applications of dynamical systems are conducted. No wonder that the word “dynamical” is a synonym of the word “can-do” in English vocabulary.
The theory of dynamical systems is powerful since it is able to qualitatively elucidate the types of solutions that nonlinear dynamical systems assume without solving them, both in “equilibrium dynamics”, i.e., when systems’ solutions converge to a steady state, and also “complex phenomena” solutions, i.e., quasi-periodic, spatiotemporal patterns, instability, and chaos.
While applications of dynamical systems are ubiquitous and you will meet them in a variety of science disciplines - from physics to chemistry to biology, most applications and examples in the literature are related to physical systems, typically described by differential or difference equations. This is not surprising since the area has been initially developed for Newtonian mechanics systems and has been extended to other physical systems, and then to other scientific disciplines.
While that has been the case so far, it might not be the case going forward. A new type of systems has emerged: Neural Networks. These are fundamental computing components of Artificial Intelligence technology that we all interact with on a daily basis. These systems are dynamic, intriguing and are not associated with physical systems directly. These systems require novel dynamical systems developments.
These are the kinds of systems and problems that my research group, UW NeuroAI, and colleagues are working on. In this article I would like to show a few examples of dynamical systems problems in Neural Networks, possible extensions of dynamical systems tools to Neural Networks, and propose future dynamical systems tools that need novel developments.
Neural Networks are Dynamical Systems
Neural Networks propagate signals through them, whether through multiple layers of Deep Neural Networks, such as ResNets, ConvNets, UNets, to name some popular architectures, or through steps of Recurrent Neural Networks. This makes these systems dynamical systems. But these are not standard dynamical systems. These systems are 1) nonlinear, 2) high-dimensional, 3) non-autonomous 4) with varying parameters. While properties 1) and 2) were part of dynamical systems studied, Neural Networks take them to the extreme. Neural Networks used in practice are highly nonlinear and of extremely high dimensionality (e.g. thousands of dimensions/variables). The complexity is extended further by property 3), since Neural Networks process data and thus the data, when given during propagation, makes them input dependent. Above all, what particularly distinguishes Neural Networks is property 4). Neural Networks undergo optimization (non-convex) in order to fit connectivity parameters to perform a particular task. Variation of parameters creates sets of systems within a system. Understanding how optimization converges to the configuration that it converges is key in Neural Networks research and practice.
Dynamical Systems Problems in Neural Networks.
Multiple problems in Neural Networks can be cast as dynamical system problems. In particular, a central problem in Neural Networks research is instability. These instabilities can arise in both forward propagation through layers, i.e., inference of a particular task in a trained network, or during back propagation (optimization) when the gradient that guides the optimization is not well defined, also known as the “vanishing/exploding” gradient problem. For these instabilities, there have been practical approaches and qualitative analyses proposed. While these provide tools for working with Neural Networks, there are still unknowns regarding instabilities. Dynamical system theory approach and its extension could contribute to more effective tools to mitigate and leverage these instabilities.
Another Achilles heel of Neural Networks is their interpretability, in terms of which features are selected and how the mapping of input to output is made. Effective interpretability is supposed to inform how the network will process a type of input beyond the particular loss function that it reports, i.e., the loss output of the network. Such a concept is abstract and thus difficult to generalize, especially approaches and visualizations that might have worked for one type of network to a variety of networks. It requires novel metrics along with analyses designed to inform about solutions of Neural Networks. This is exactly what dynamical systems theory was able to propose for differential and difference equations, in the form of embeddings, measures, estimates, mappings, expansions and so on.
Stability and Lyapunov Exponents for RNNs
An example of application of dynamical systems to Neural Networks is our work on Lyapunov Exponents Interpretation for Recurrent Neural Networks (RNNs). This direction was Ryan Vogt PhD thesis, UW AMATH PhD student in UW NeuroAI, graduated this Spring.
RNNs specialize in processing sequential data, such as natural speech or text, and broadly, multivariate time series data. RNNs can be defined as dynamical systems of the type
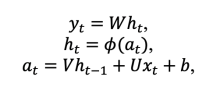
where the vectors xt, ht, at, yt are vector fields such that xt is the vector of inputs into the network, ht is the vector of hidden states, at is the activation vector, yt is the vector of outputs, at step t, and b is the bias vector.
While RNN are ubiquitous systems, these networks cannot be easily explained in terms of the architectures they assume, the parameters that they incorporate, and the learning process that they undergo. A powerful dynamical system method for characterization and predictability of dynamical systems is Lyapunov Exponents (LE) [1,2], which capture the information generation by a system's dynamics through the measurement of the separation rate of infinitesimally close trajectories. LEs i are defined as
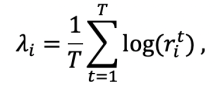
where rit is the ith diagonal term in matrix R (expansion coefficient) obtained from QR decomposition of the Jacobian of the hidden states at step t. The number of steps T is expected to be long enough such that i converge.
The collection of all LE is called LE spectrum. Numerical algorithms have been developed for LE spectrum computation. These have been applied to various dynamical systems including hidden states of RNN and variants such as LSTM and GRU [3]. While RNNs are non-standard dynamical systems, the approach recalls the theory related to random dynamical systems that establishes LE spectrum even for a system driven by a noisy random input sequence sampled from a stationary distribution [4].
In collaboration with Guillaume Lajoie, UW AMATH Alum, now Associate Professor at UdeM and Mila, and Maximilian Puelma Touzel, Research Associate at Mila, our work demonstrated that some features of LE spectra can have meaningful correlation with the performance of the corresponding networks on a given task [5].
The Future is Dynamical
Examples in [5] suggested that features of LE spectrum are correlated with RNN robustness and accuracy, but which features can be utilized for RNN analysis? Standard features, such as maximum and mean LE can have weak correlation, making consistent characterization of network quality using a fixed set of LE features unfeasible.
In a subsequent work, Ryan Vogt and Yang Zheng, UW ECE PhD student in UW NeuroAI group, proposed a data driven methodology, called AeLLE, to infer LE spectrum features and associate them with RNN performance. The methodology implements an Autoencoder (Ae) which learns through its latent units a representation of LE spectrum (LLE) and correlates the spectrum with the accuracy of RNN for a particular task. The latent representation appears to be low dimensional and interpretable such that a simple linear embedding of the representation corresponds to a classifier for selection of optimally performing parameters of RNN based on LE spectrum [6]. Essentially, it’s a Neural Network that learns to embed features of LE of Neural Networks!
Such an approach is only the tip of the iceberg in possibilities that dynamical systems theory could unlock in the study of Neural Networks. One could attempt extending such embeddings toward effective choice of network architecture, pruning networks, selecting hyperparameters in more optimal way, etc. These are key problems in Neural Networks. Furthermore, it is intriguing to develop dynamical system tools that will inform and guide Neural Networks optimization. Extension of dynamical systems tools to deal with variation of parameters will not only contribute to novel approaches in Neural Networks, but also develop novel chapters of dynamical systems theory motivated by Neural Network Mechanics.
References
[1] Valery Oseledets (2008), Scholarpedia, 3(1):1846.
http://www.scholarpedia.org/article/Oseledets_theorem
[2] Ruelle, D.: Ergodic theory of differentiable dynamical systems. Publications Mathématiques de
l’Institut des Hautes Études Scientifiques 50(1), 27–58 (1979)
[3] Engelken, R., Wolf, F., Abbott, L.F.: Lyapunov spectra of chaotic recurrent neural networks. arXiv
preprint arXiv:2006.02427 (2020)
[4] Arnold, L.: Random dynamical systems. Dynamical systems, 1–43 (1995)
[5] Vogt, R., Puelma Touzel, M., Shlizerman, E., Lajoie, G.: On Lyapunov exponents for RNNs:
Understanding information propagation using dynamical systems tools. Frontiers in Applied Mathematics
and Statistics 8 (2022)
[6] Vogt, R., Zheng, Y., Shlizerman, E. Lyapunov-Guided Representation of Recurrent Neural
Network Performance, in review (2023)